[Lecture Notes] ShanghaiTech CS252 Cryptography
Lecture 1
Information security
The protection of information and information systems from unauthorized access, use, disclosure, disruption, modification, or destruction in order to provide confidentiality, integrity, and availability.
Confidentiality: the property that sensitive information is not disclosed to unauthorized individuals, entities, or processes.
Integrity: the property that sensitive data has not been modified or deleted in an unauthorized and undetected manner.
Authentication: the process of establishing confidence in the identity of users or information systems.
Non-Repudiation: assurance that the sender of information is provided with proof of delivery and the recipient is provided with proof of the sender’s identity, so neither can later deny having processed the information.
Course outline
- classical cryptography
- private-key cryptography
- public-key cryptography
- advanced topics
Lecture 2
Private-key Encryption (PrivKE)
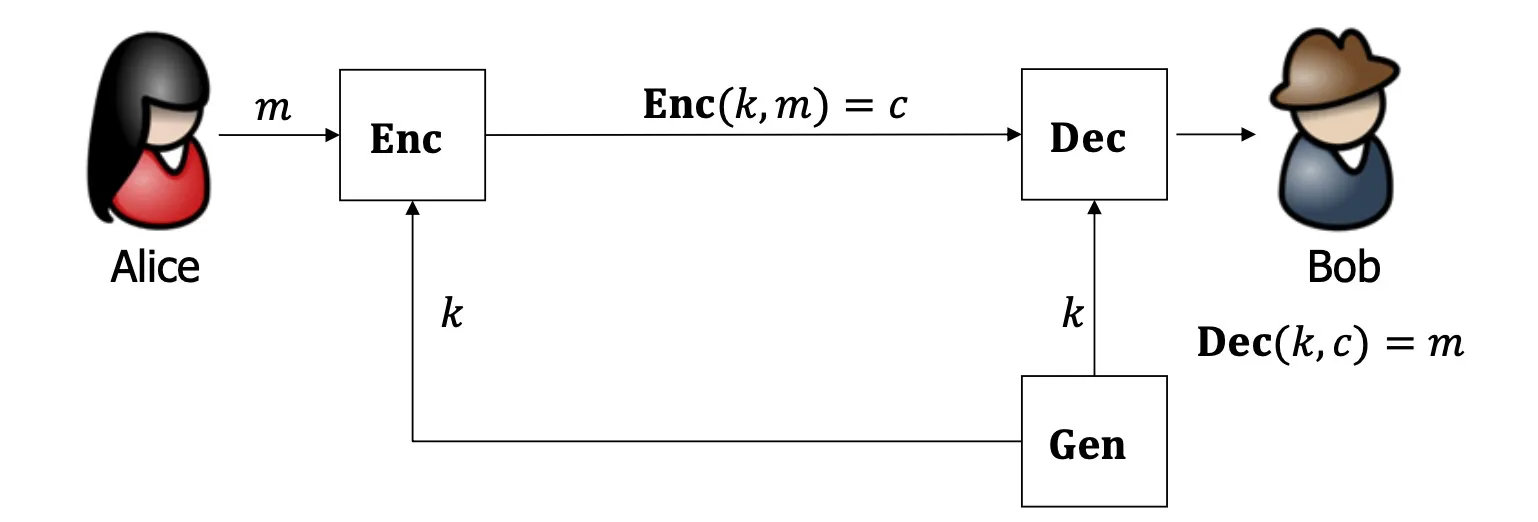
- = key generation, = encryption, = decryption
- = secret key, = plaintext (message), = ciphertext
- = key space, = plaintext space, = ciphertext space
- Correctness:
- Security: the adversary should not be able to learn from
Kerchkhoff’s Principle
Kerchkhoff’s Principle: The cipher method must not be required to be secret, and it must be able to fall into the hands of the enemy without inconvenience.
Kerchkhoff原则: 加密算法应该公开, 唯一需要保密的是通信双方共享的秘密密钥.
Shift Cipher 移位加密
Scheme:
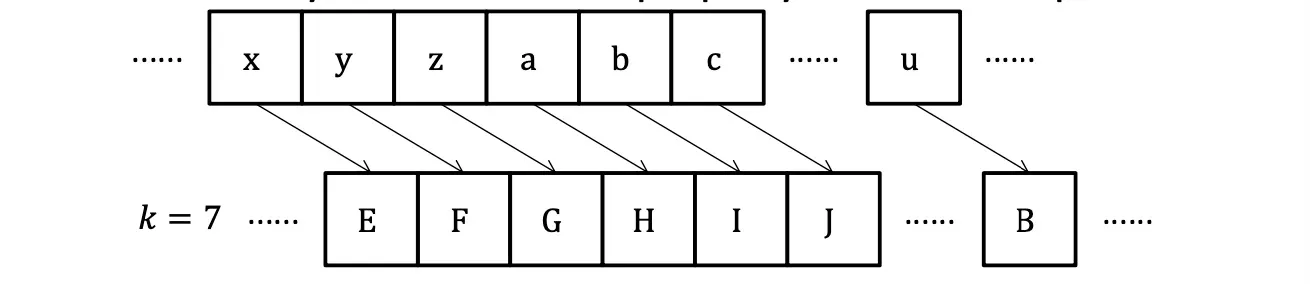
Brute-force attack 穷举法攻击
Brute-force attack / Exhaustive attack: try all possible secret keys
Sufficient Key Space Principle: key space should be large enough
密钥空间充分性原则: 任何安全的加密方案必须拥有一个能够抵御穷举搜索的密钥空间
Improved attack
Drawbacks of brute-force attack: difficult for a computer to check whether a given text “makes sense”. => Improved and automated attack:
= the frequency of the -th letter in a normal English text 英文中字母出现的频率
= the frequency of the -th letter in the ciphertext
Idea: Find the secret key such that (the most closest to 0.065)
Substitution Cipher 单字母替换加密
Scheme:

Key space is large for brute-force attack.
Still not secure! Can be broken letter frequency analysis. 可通过字母频率破解.
Vigenere Cipher 多字母移位加密
Scheme: = the letter obtained by shifting forward positions

Key space is infinite in theory. In addition, same letter in plaintext can be mapped into different letters in ciphertext
Still not secure!
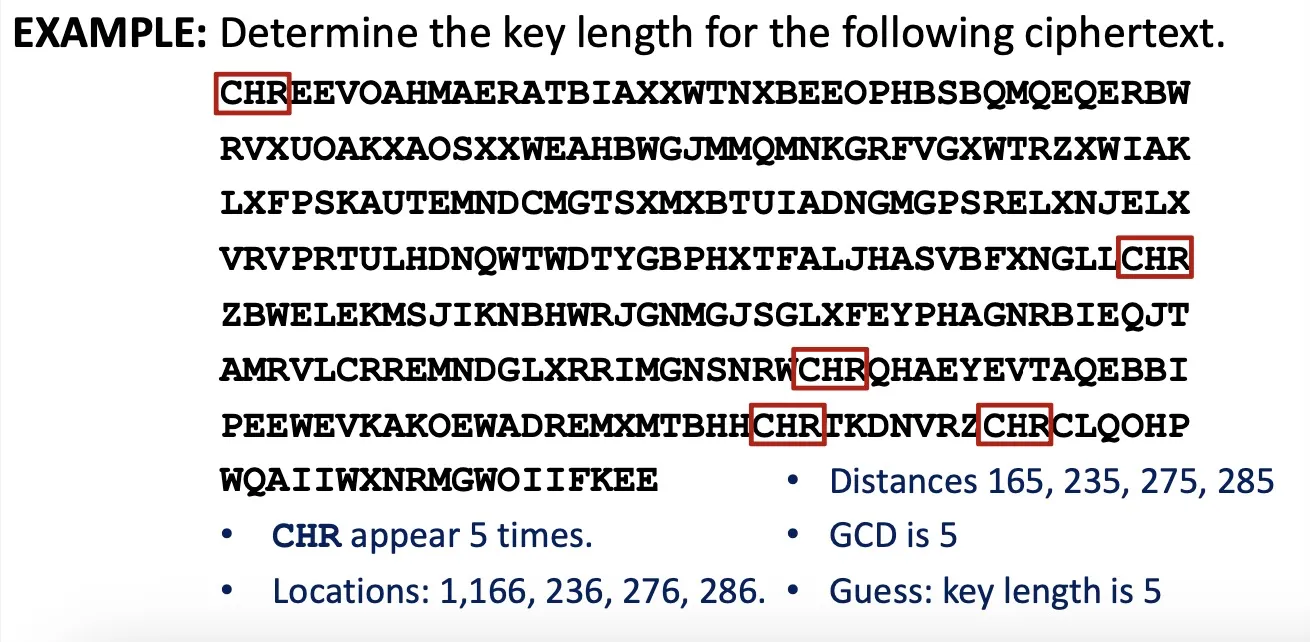
Kasiski’s method: two identical segments of plaintext may be encrypted to same ciphertext if their distance is a multiple of key length .
Search for pairs of identical segments → record distances → calculate GCD
Find the key length and then break shift ciphers.
Lecture 3.
Classical & Modern Cryptography
- Modern cryptography: a science
- Principles: 现代密码学的三个原则
- Formal definitions of security 形式化的安全定义
- Precise assumptions 准确的假设
- Proofs of security 严格的安全证明
- Principles: 现代密码学的三个原则
Formal definitions of security
Good definition: It should be impossible for an adversary to learn any additional information of from .
Security Guarantee
如果没有敌手能够从密文中计算任何关于明文的函数,则加密方案是安全的.
Threat model: defines the power of the adversary
Typical threat models for private-key encryption (COA, KPA, CPA, CCA)
Ciphertext-only Attack (COA) 密文攻击
- Adversary observes ciphertext
- It tries to determine the plaintext
- 最基本的攻击方式: 敌手只能观察到密文, 试图确定对应的明文
Known-Plaintext Attack (KPA) 已知明文攻击
- Adversary learns pairs of plaintext and ciphertext generated using some key
- It tries to determine information about the plaintext of some other ciphertext produced using the same key.
- 敌手学习一个/多个使用相同密钥加密的明文/密文对, 目标是确定其它使用相同密钥加密的密文对应的明文
Chosen-Plaintext Attack (CPA) 选择明文攻击
- Adversary obtains plaintext/ciphertext pairs for plaintexts of its choice
- It tries to determine the plaintext of some other ciphertext produced using the same key.
- 攻击者能够选择一段明文, 得到密文; 试图确定其它密文对应的明文
Chosen-ciphertext Attack (CCA) 选择密文攻击
- Adversary obtains plaintext/ciphertext pairs for plaintexts/ciphertexts of its choice.
- It tries to determine plaintext of some other ciphertext produced using the same key
- 敌手不仅能做CPA(选择一段明文获得密文), 还能选择一段密文获得明文; 试图确定其它密文对应的明文
A security definition looks like: a cryptographic scheme for a given task is secure if no adversary of a specific power (指定攻击者的power) can achieve a specified break (指定攻击类型).
Precise Assumptions
Assumption (假设): Statements that are not proven but conjectured to be true 未经证明但猜测为真的命题
E.g The integer factoring problem / discrete logarithm problem is hard.
(The integer factoring problem 大整数分解问题)
Proofs of security
Provable security: If the designed cryptographic scheme can be broken by an adversary, then the underlying assumption is false. (类似于反证法: 假设方案不安全,adv能攻破,推出assumption不成立)
If the scheme is not secure, then a well-known hard problem can be solved in polynomial time.
Lecture 4.
Distributions on
- Secret Key : output of , an r.v. taking values in
- , determined by key generation algorithm
- e.g. is uniform (均匀分布) in shift cipher / substitution cipher
- Plaintext :
- , determined by sender’s preference (明文的先验概率)
- Ciphertext : output of
Fundamental assumption: K,M are independent random variables.
基本假设: K M 独立 (密钥和明文是独立选择的)
Perfect Secrecy 完善保密性
Definition: is perfectly secret if
distribution , , with ,
Perfect secrecy requires to be independent
明文的概率分布和密文概率分布无关
For simplicity, assume
Security guarantee: The adversary learns no additional information about given .
敌手获得密文c之前和之后,对明文m的认识没有改变(对明文m的后验概率分布和先验概率分布一致)
Theorem: is perfectly secret if and only if
One-Time Pad 一次一密
Scheme:
- : (二进制比特串 例如10010101100101)
- : (密文是明文和key逐bit取异或)
- :
Theorem: one-time pad is perfectly secret.
Drawbacks:
long secret key (as long as message) 密钥长度与明文长度相同, 太长了
Kerckhoffs (是Kerckhoff提出的另一个原则): It must be possible to communicate and remember the key without using written notes, and correspondents must be able to change or modify it as will.
密钥不能太长, 太长了记不住, 不方便交换和更改密钥
one-time security: same key cannot be used more than once
两条消息使用同一个密钥加密, 敌手能算出两条消息异或的结果
Limitations Of Perfect Secrecy 完善保密性的局限
Theorem: perfectly secret encryption,
完善保密的加密方案,密钥空间明文空间
Perfect Indistinguishability 完美不可区分性
Let be a private-key encryption.
Define an adversial indistinguishability experiment (敌手不可区分实验)
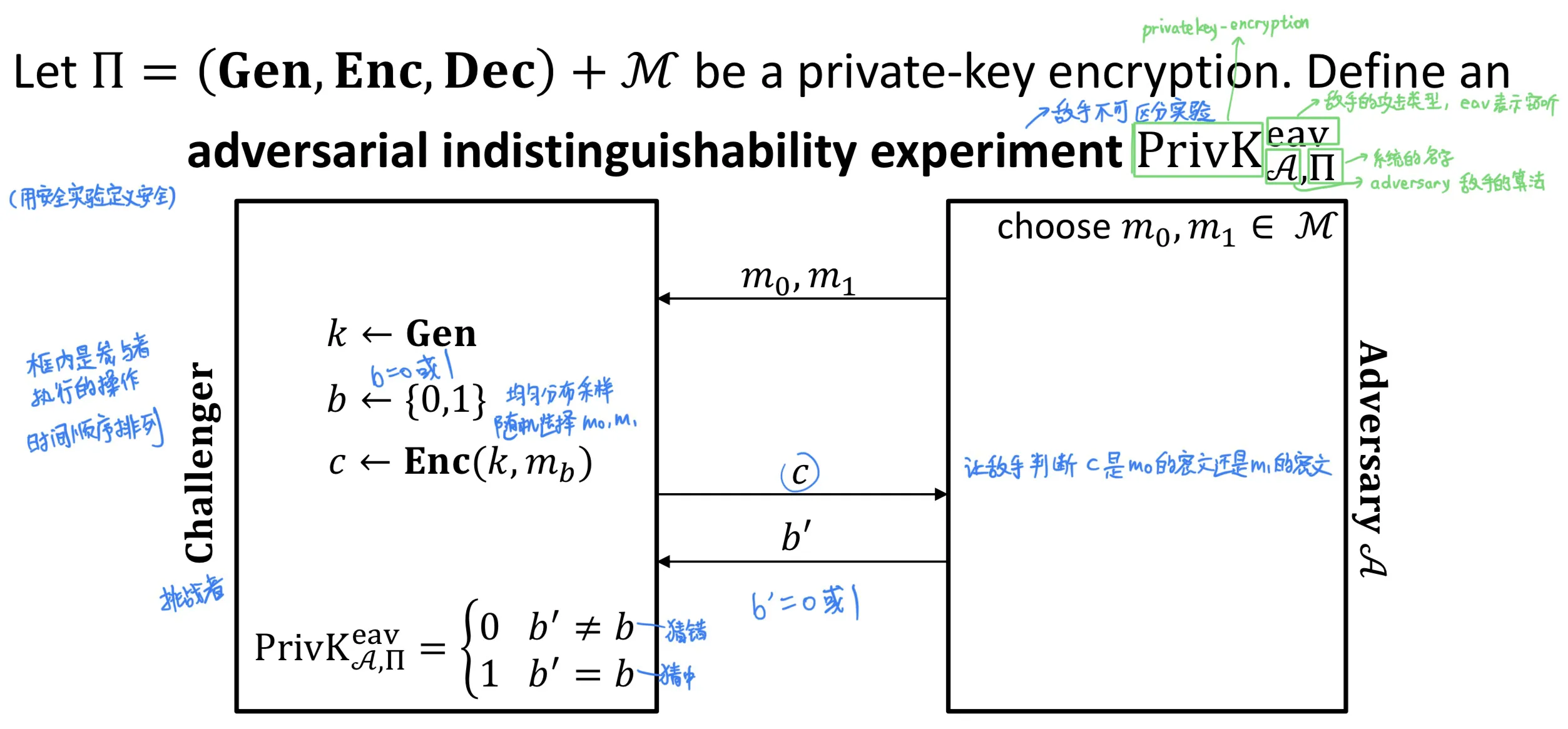
步骤:
- (1) 敌手输出一堆长度相等的消息
- (2) 选或进行加密, 让敌手判断这条密文是还是加密得来的
Definition: is perfectly indistinguishable if for every adversary ,
(完美不可区分的定义: 敌手不可区分实验中猜对的概率是1/2)
Theorem: is perfectly secret iff is perfectly indistinguishable.
完善保密 当且仅当 完美不可区分
Lecture 5.
Computational Security 计算安全
Computational security: two relaxations for practical encryption
Security is only guaranteed against efficient adversaries that run for some feasible amount of time
敌手的计算能力有限
Adversaries can potentially succeed with some very small probability
攻破的概率足够小即可
定义计算安全的两种方式:具体方式 concrete approach; 渐进方式 asympotic approach
Concrete Approach
A scheme is -secure if any adversary with running time can succeed in breaking the scheme with probability .
运行时间最多为 的敌手攻破的概率小于
PPT and Negligible
Polynomial-time algorithm 多项式时间的算法
PPT: probabilistic polynomial time 概率多项式时间
Negligible: A function is negligible if for any polynomial function , there exists such that for all
函数可忽略的定义: 对于足够大的n, f(n)的值小于任何一个多项式函数
e.g. is negligible
e.g. is not negligible
等价表述: 对所有常量, 存在一个 使得对于所有 , .

Theorem: Let be negligible and let be a polynomial, then , are both negligible.
Asymptotic Approach
A scheme is secure if any PPT adversary can succeed in breaking the scheme with at most negligible probability.
如果每个PPT敌手以可忽略函数的概率成功攻破,那么加密方案是安全的
Lecture 6.
IND-EAV
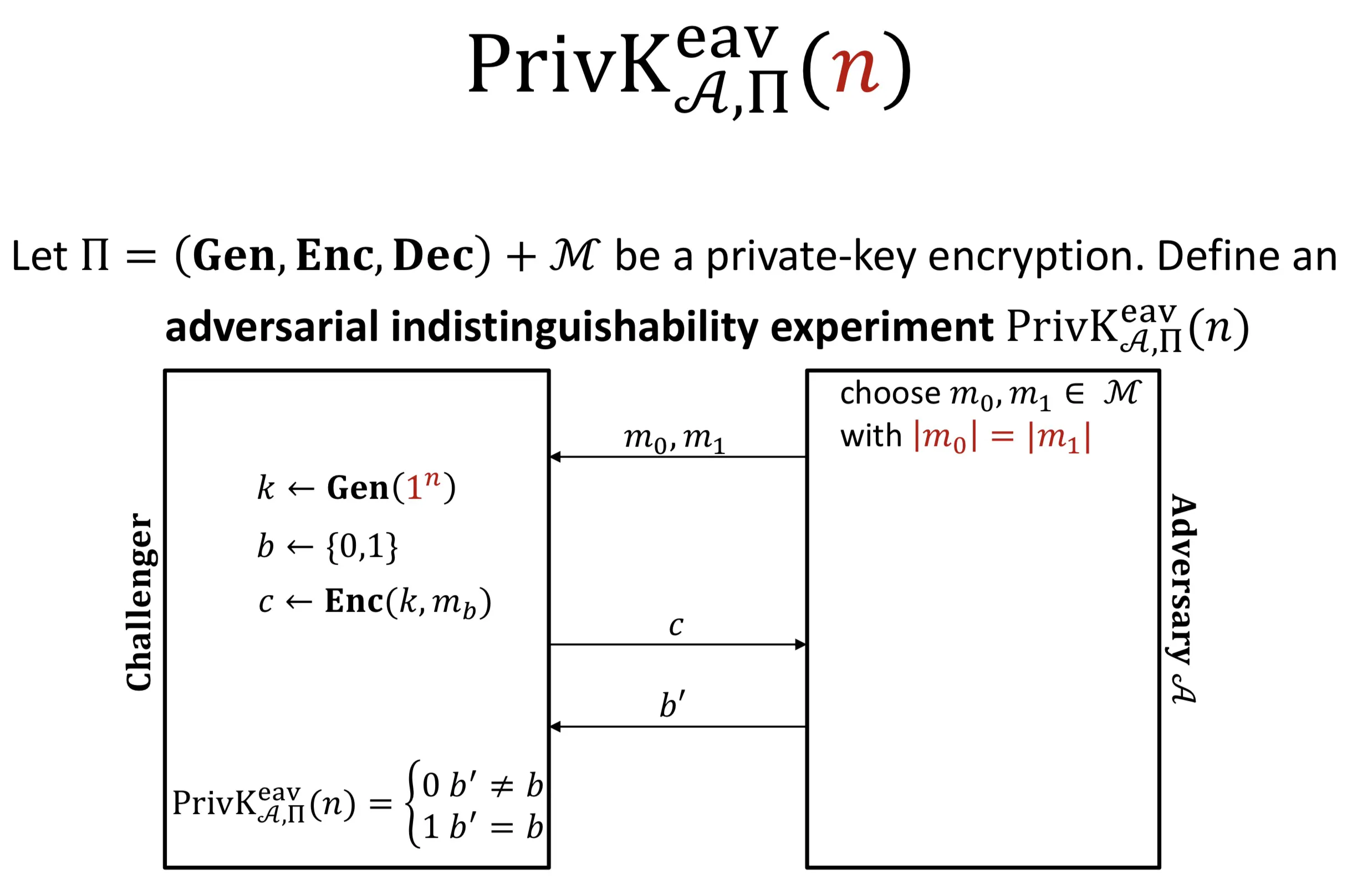
Indistinguishable encryption in the presense of an eavesdropper (IND-EAV) 窃听者存在情况下的不可区分性
Definition (IND-EAV1): for all PPT adversaries there is a negligible function such that
Definition(IND-EAV2): for all PPT adversaries there is a negligible function such that
Theorem: IND-EAV1 if and only if IND-EAV2
OTP is IND-EAV
One time padding 具有窃听者存在情况下的不可区分性
Statistical distance
Definition: statistical distance between random variables that take values in set :
Lecture 7.
Computational indistinguishability 计算不可区分性
Definition: for any PPT distinguisher ,

Pseudorandomness 伪随机性
Definition: be uniformly distributed over , is pseudorandom if and are computationally indistinguishable.
伪随机性的定义: 的分布与均匀分布(随机比特串)计算不可区分.
PRG (Pseudorandom Generator)
Definition: A function is called a PRG if it satisfies the following:
effiently computable: 对所有, 多项式时间可以算出
expansion:
pseudorandomness: is pseudorandom
( 与真正的随机字符串 不可区分)
Fixed-length encryption from PRG

Theorem: If is a PRG, then IND-EAV secure.
Lecture 8.
One-way function (OWF)
Definition: easy to compute + hard to invert 正向容易计算, 反向求逆困难
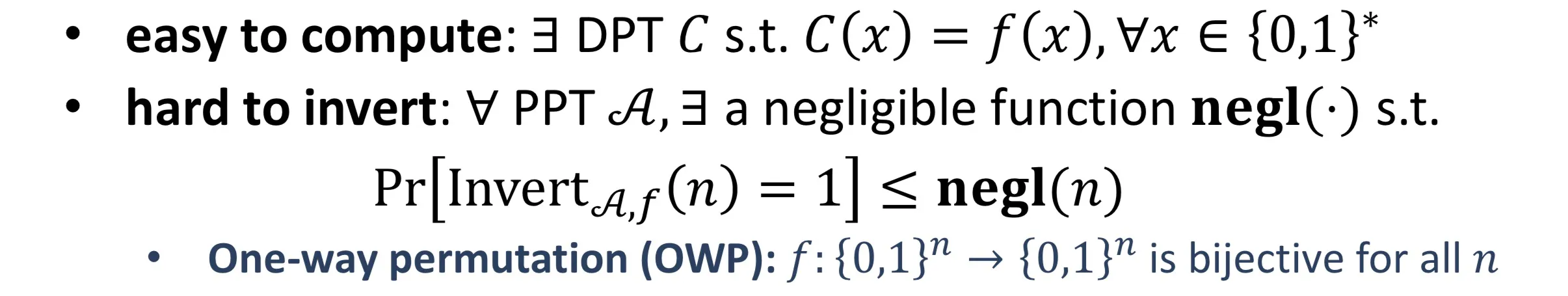
Inverting experiment

Hard-Core Predicate (HCP)
Definition:

Goldreich-Levin Theorem: Assume that OWFs (OWPs) exist. Then there is a OWF (OWP) and a hard-core predicate for .
Theorem: Let be a OWP and let be a hard-core predicate for . Then is a PRG.
IND-m-EAV
Multiple-message eavesdropping experiment
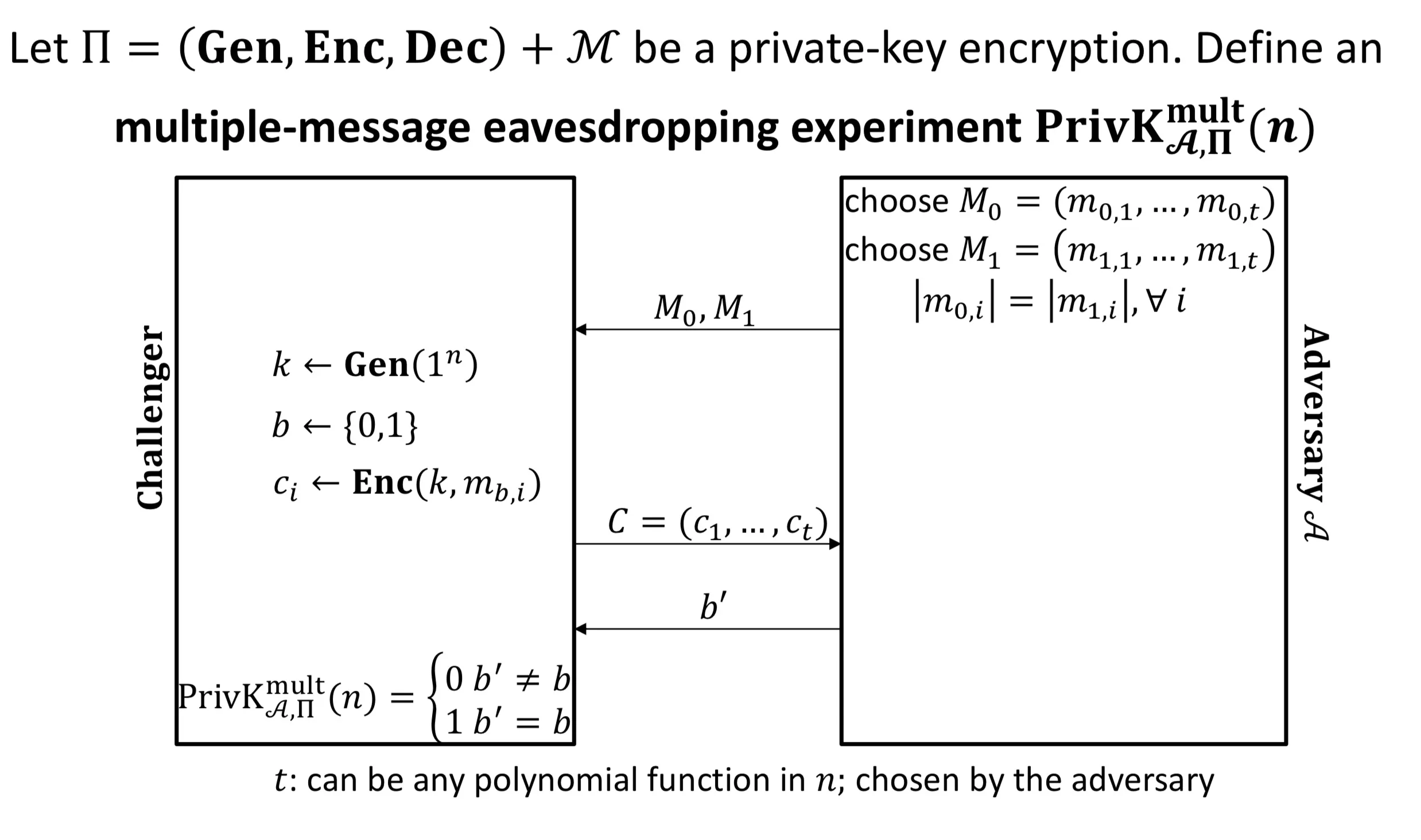
indistinguishable multiple encryptions in the presence of an eavesdropper (IND-m-EAV)

IND-m-EAV IND-EAV (IND-m-EAV是IND-EAV t=1时的特例)
Theorem: If is stateless and is deterministic, then not IND-m-EAV secure.
- stateless: each invocation of and is independent of all prior invocations
- deterministic: no random numbers used
- (To be IND-m-EAV secure, must either be stateful or probabilistic)
IND-CPA
CPA indistinguishability experiment
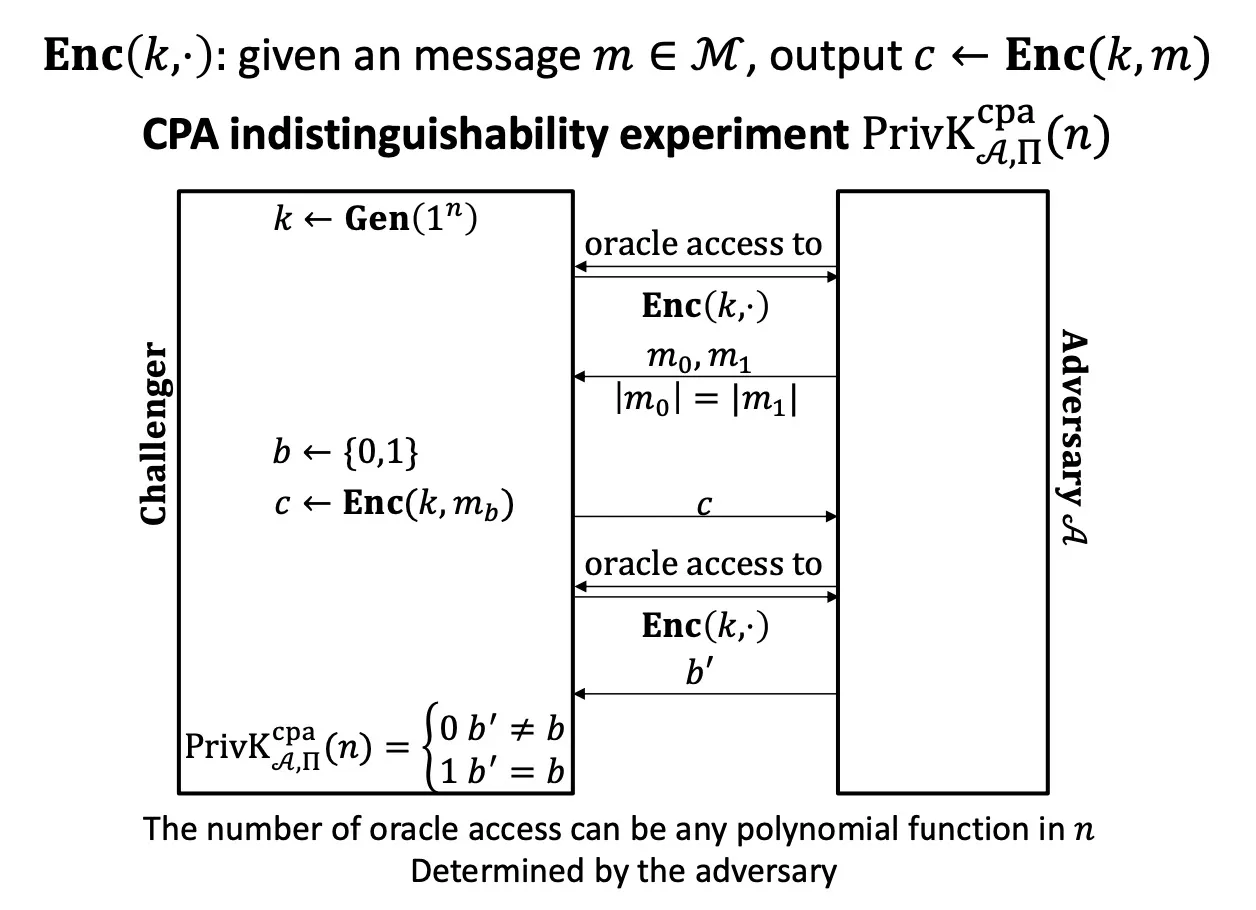
indistinguishable encryptions under a chosen-plaintext attack

IND-m-CPA
LR-Oracle experiment

insidtinguishable multiple encryptions under a chosen-plaintext attack

IND-m-CPA IND-CPA
IND-m-CPA IND-m-EAV
IND-CPA IND-m-CPA
Lecture 9.
Pseudorandom Function (PRF)
Definition: , 第一个输入是key
- length-preserving: key、输入输出长度相等
- PRF: 与真随机函数 computationally indistinguishable

Lecture 10.
IND-CPA from PRF

PRGPRF, PRFPRG

PRP and sPRP

Lecture 11.
ECB, CBC, OFB, CTR
ECB
Electronic Code Block
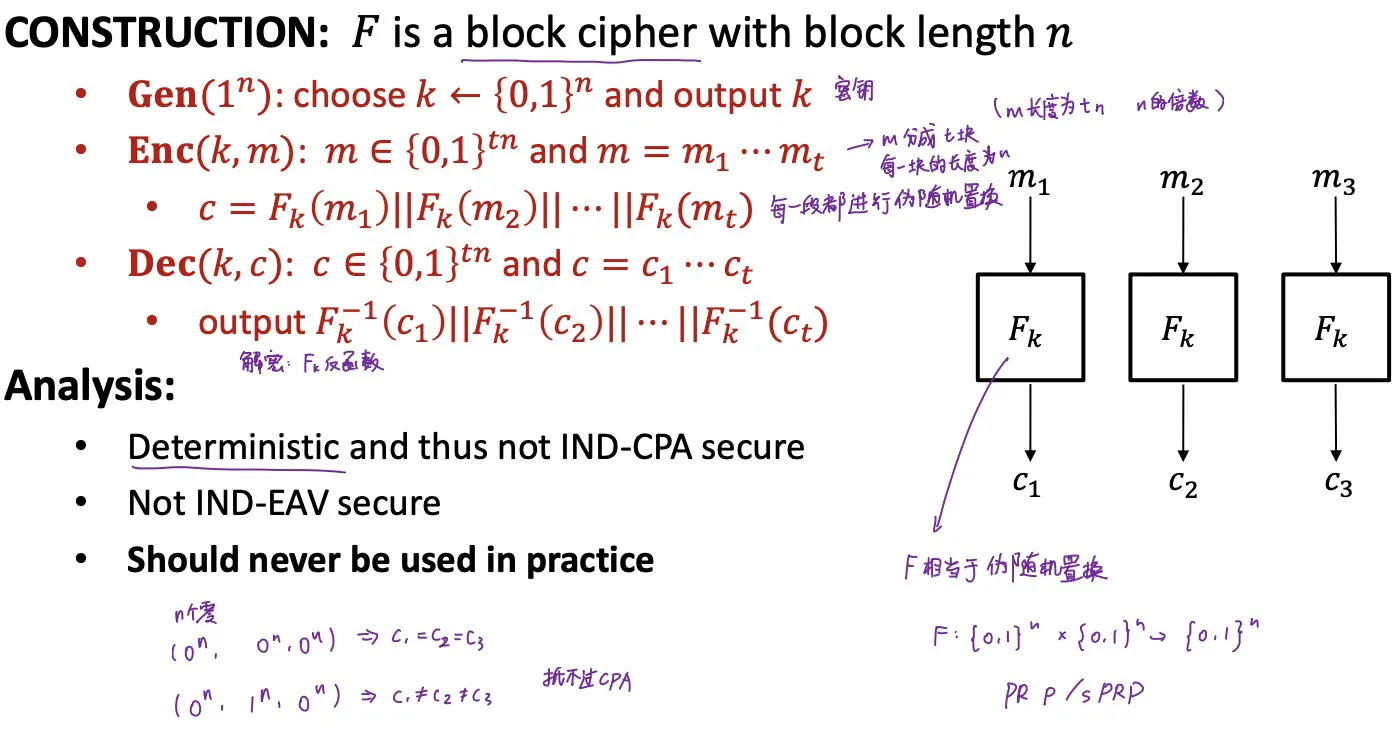
ECB is not IND-CPA secure; not IND-EAV secure
CBC
Cipher Block Mode
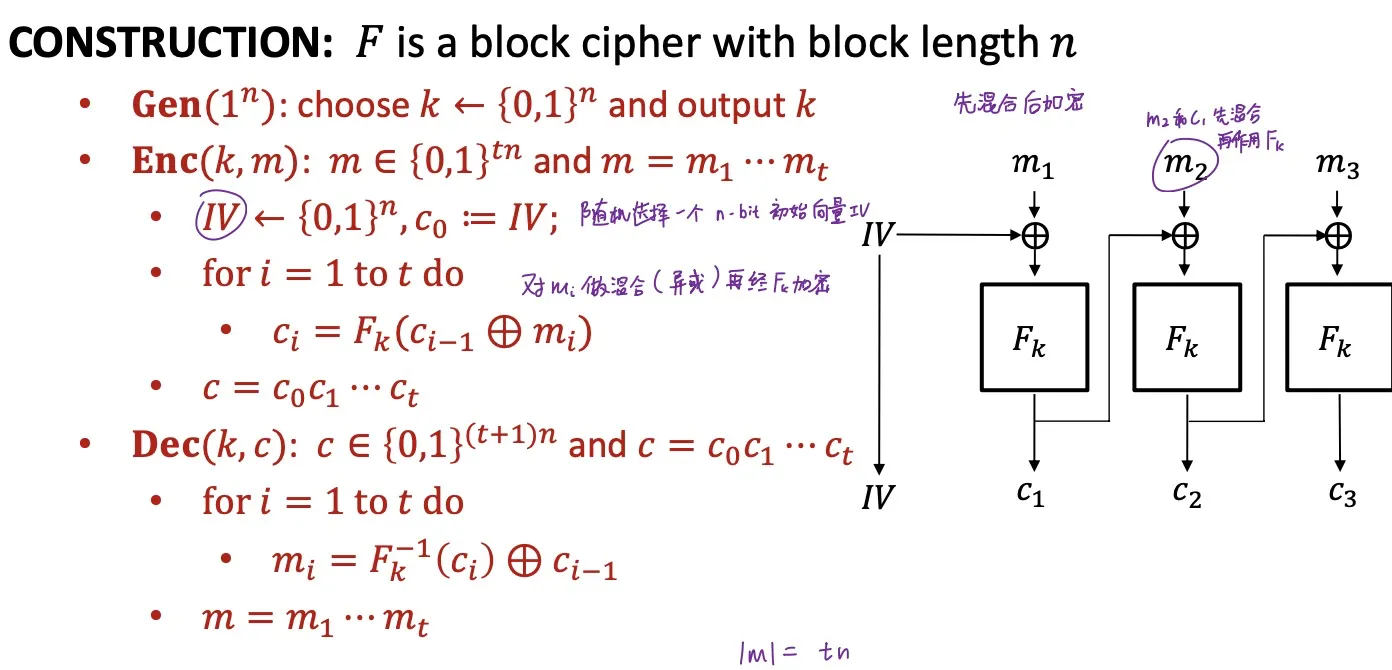
CBC is IND-CPA secure (if is a PRP)
The (initialization vector) must be chosen uniformly at random.
e.g. 如果是计数器 (用加密第条明文), 则不IND-CPA secure)
必须顺序执行,不能并行
Chained CBC
把上一条密文的最后一个ciphertext block当做下一条明文的
not IND-CPA secure.
OFB
Output Feedback Mode
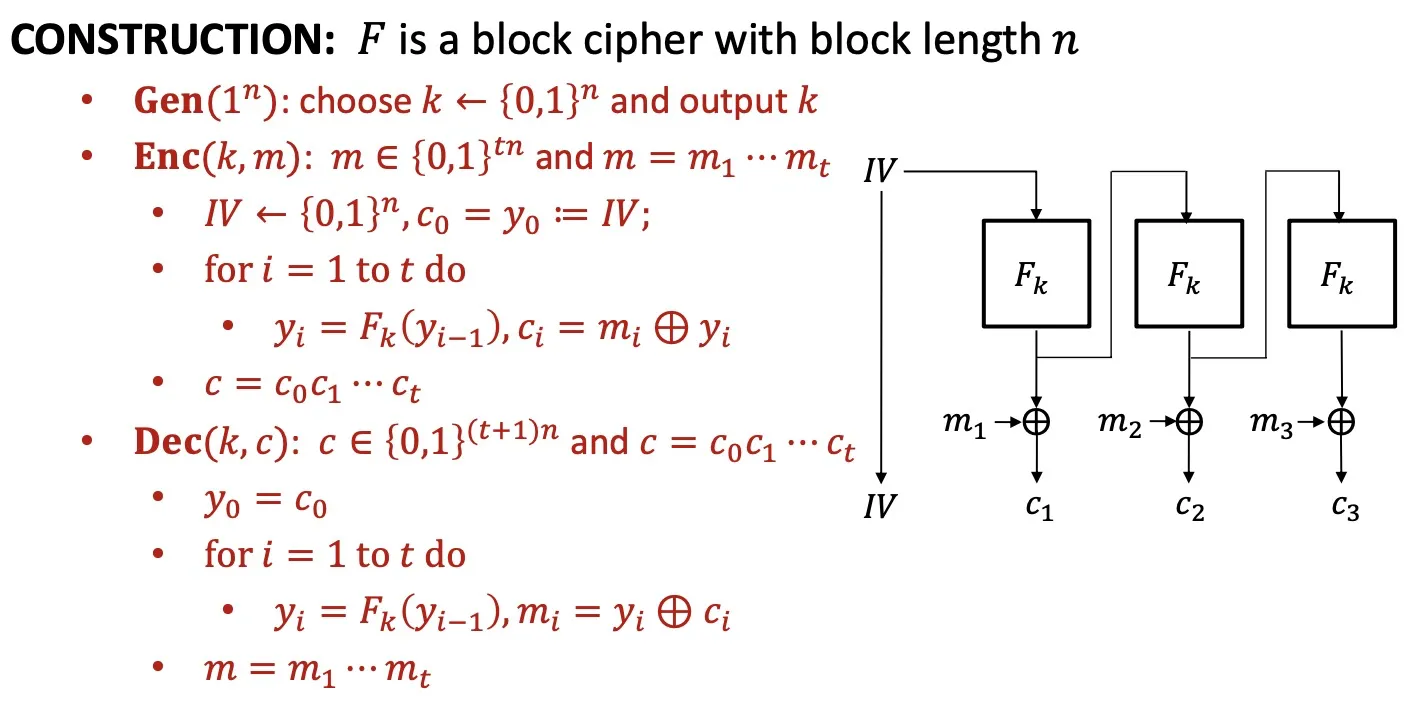
- OFB is IND-CPA secure (if is a PRF)
- 不能重复使用
CTR
Counter
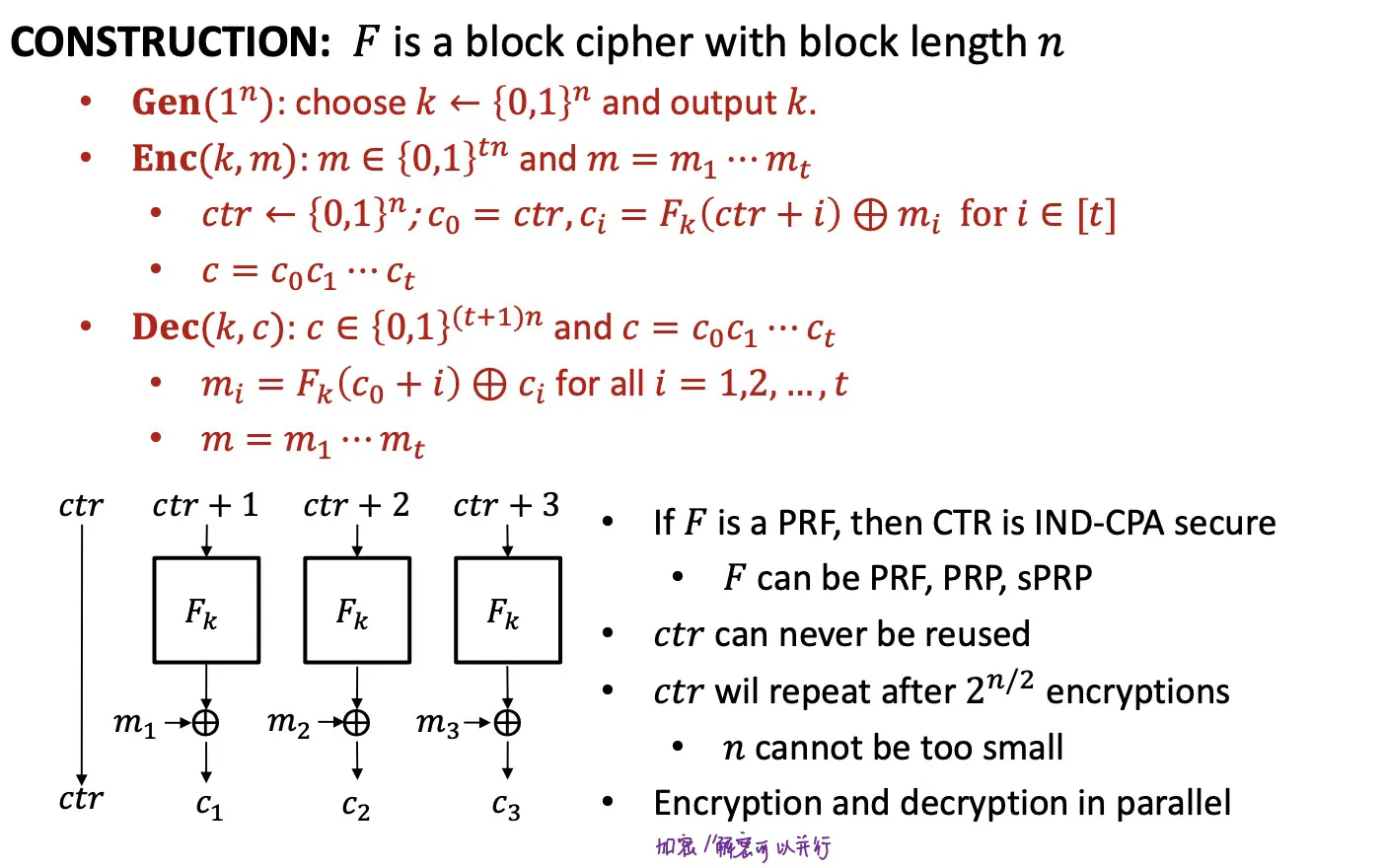
- CTR is IND-CPA secure (if is a PRF)
Lecture 12.
Message Authentication Code (MAC 消息鉴别码)
Definition: =(Gen, Mac, Vrfy)
- Correctness: Vrfy(k, m, Mac(k,m)) = 1
Message Authentication Experiment:
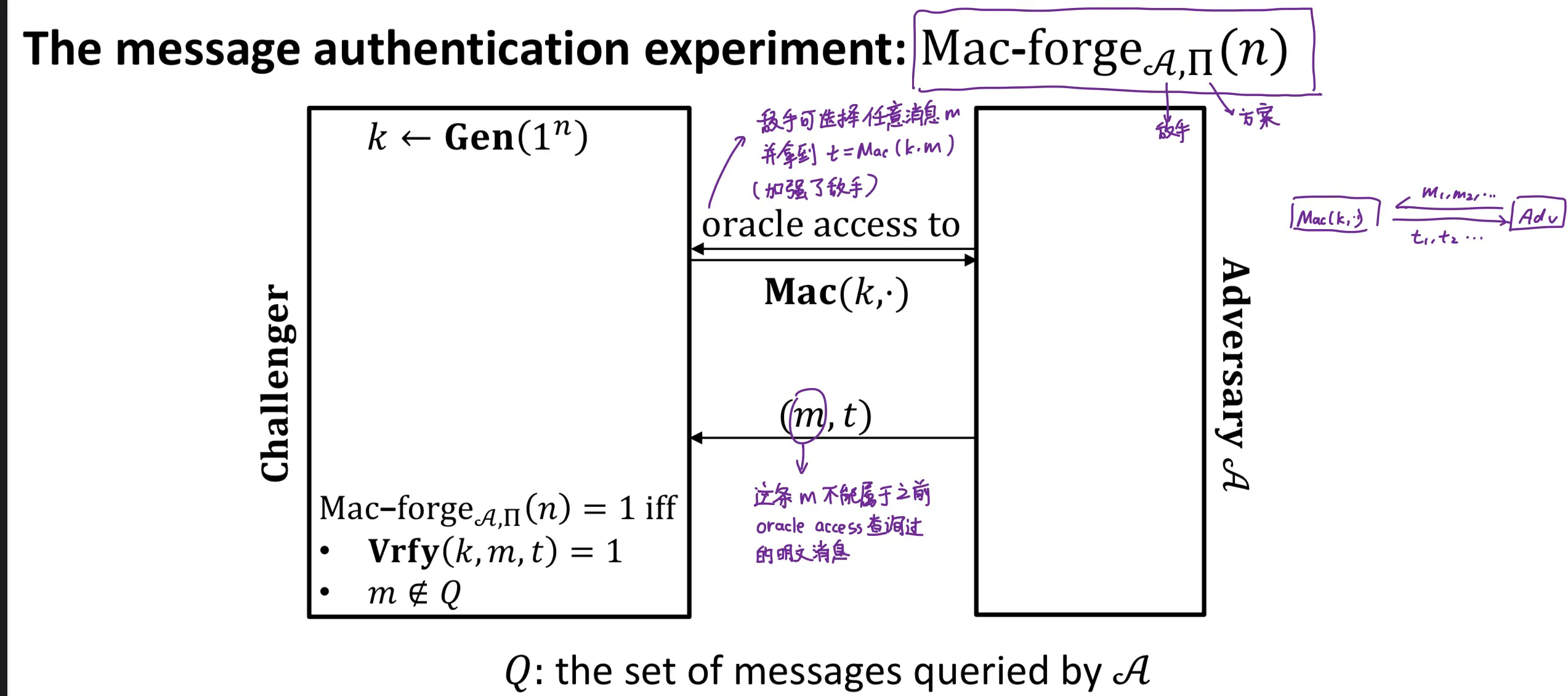
EUF-CMA
Definition: is existentially unforgeable under an adaptive chosen-message attack (EUF-CMA) (自适应选择消息攻击下的存在性不可伪造性) if for all PPT adversary,
Replay attack: adversary intercept and send it again 敌手可能会发送以前oracle access试过的消息重发一遍
- sequence numbers / time stamp (send instead of )
可通过给消息加序列号/时间戳防止replay attack
Fixed-Length MAC from PRF
Construction:
- : , a length-preserving PRF
- (fixed-length MAC generated from PRF )
Theorem: If is a PRF, then is EUF-CMA
Arbitrary-Length MAC
Idea
, ,
Idea 1:
Block re-ordering attack: 敌手改变分块顺序
解决方法: Idea 2 把块的序号加上
Idea 2:
其中 是消息的第几块的序号 (从到)
Truncation attack: 敌手从末尾丢弃分块
解决方法: Idea 3 把消息总长加上
Idea 3:
- 其中 是整个消息的长度,
Construction

Fixed-length CBC-MAC
Construction:
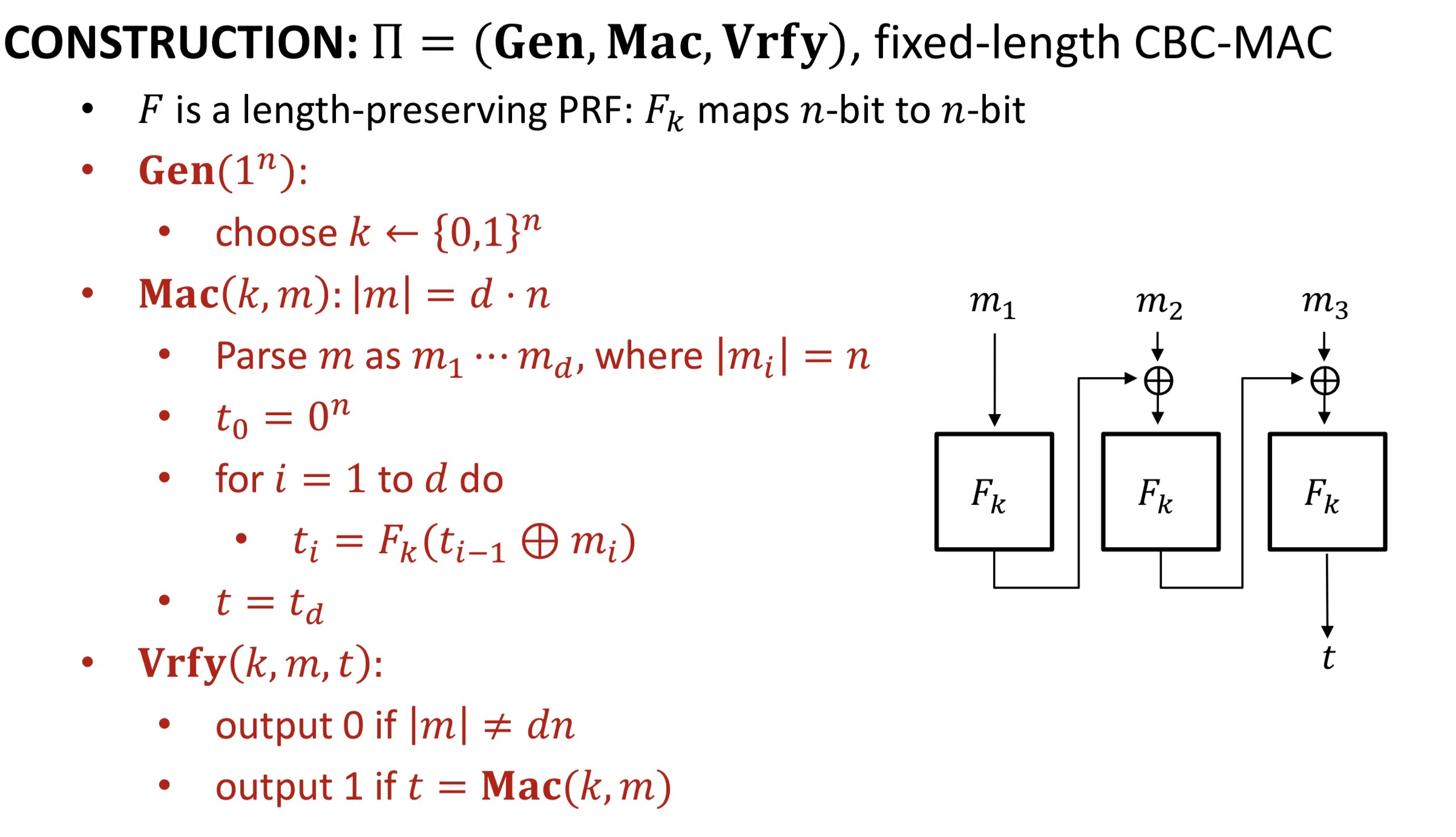
Theorem: If is a PRF, then EUF-CMA secure for messages of length .
如果F是PRF,那么上面的方案EUF-CMA安全,但是必须确定.
Arbitrary-length MAC
TODO
Lecture 13.
sEUF-CMA
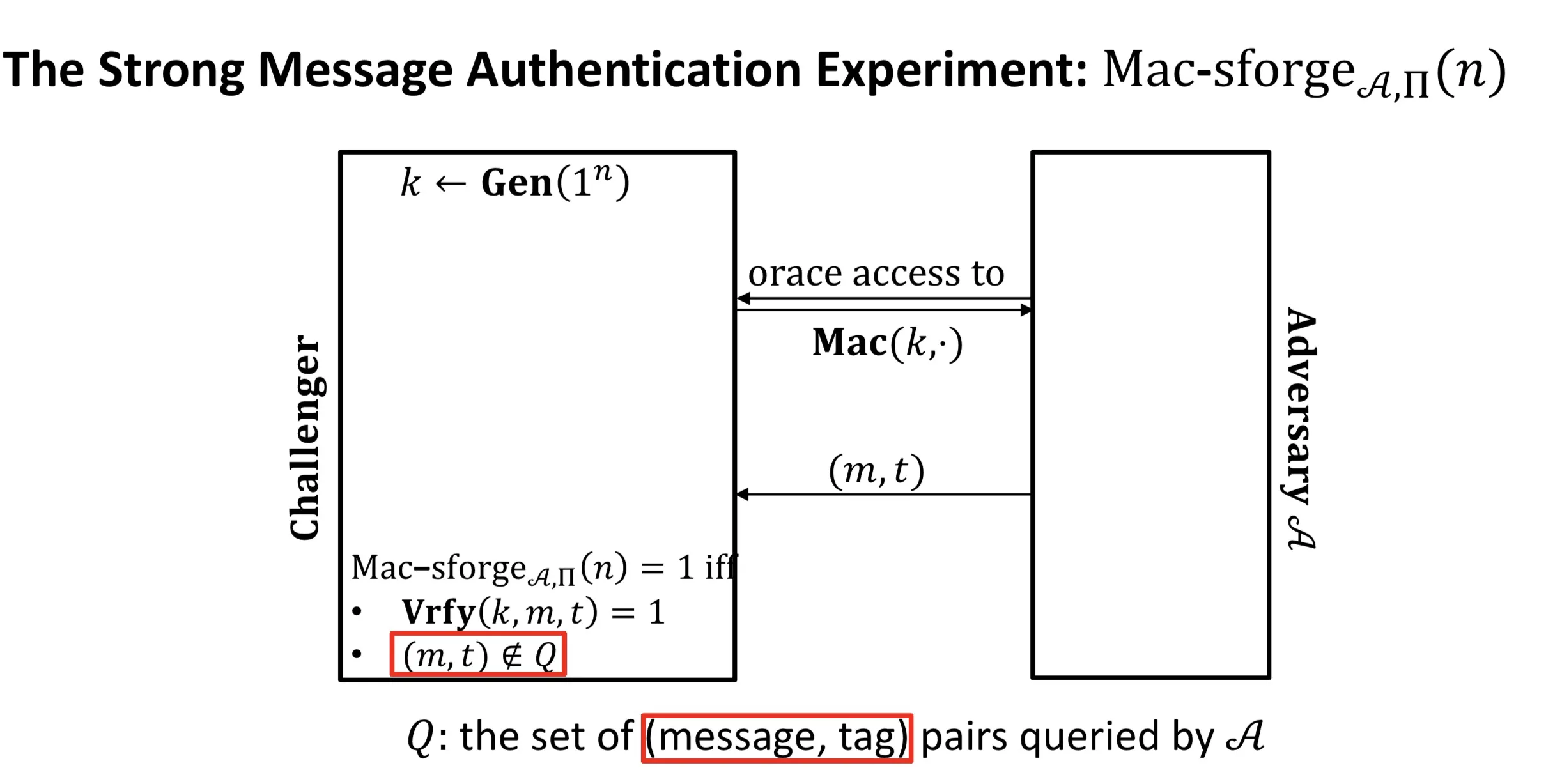
与EUF-CMA的不同: EUF-CMA是 (不能使用被查询过的明文), 这里和都.
sEUF-CMA EUF-CMA.
IND-CCA
Chosen-ciphertext attack 选择密文攻击
CCA Indistinguishability experiment CCA不可区分实验: 敌手oracle access能够选择任意明文加密, 选择任意密文解密。敌手发送两条消息, 判断哪一条消息被加密了

IND-CCA: has indistinguishable encryptions under a chosen-ciphertext attack (IND-CCA) if 实验成功概率
IND-CCA IND-CPA
OTP is not CCA
One time padding:
Attack via Malleability: (先用oracle access查询全0和全1的加密结果, 再改变一个bit生成新的消息)

Hash function
Definition: a hash function is a pair of PPT algorithms
- 生成key: (生成出来的密钥是公开的)
- 哈希函数:
- 如果哈希函数的输入长度固定 (fixed-length hash function), , 则也叫 compression function
Collision Resistance
Collision-Finding experiment:
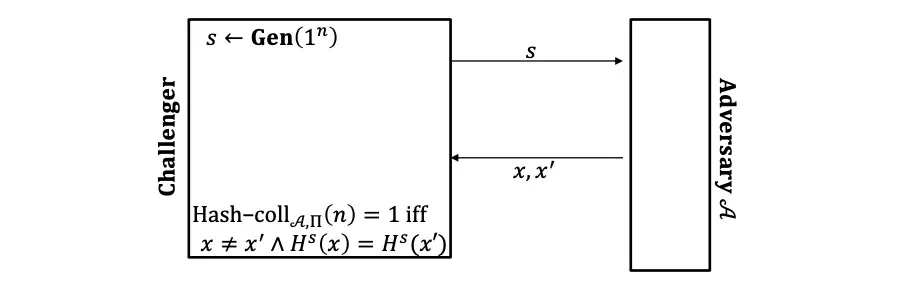
Collision-resistant:
抗碰撞: 敌手发现哈希碰撞的概率要小于
Second-Preimage Resistance
Second Preimage-Finding experiment:
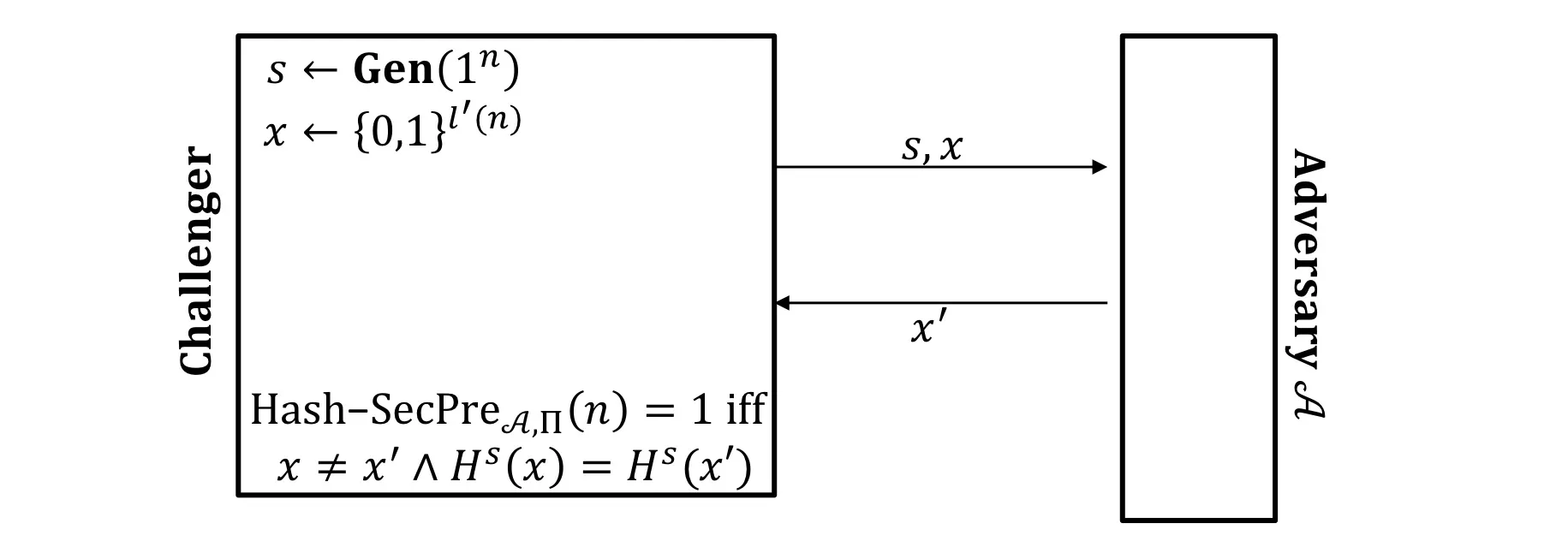
Second Preimage resistant:
给定, 敌手找到另一个 使得 与哈希值相同的概率小于negl(n)
Preimage Resistance
Preimage-Finding experiment:
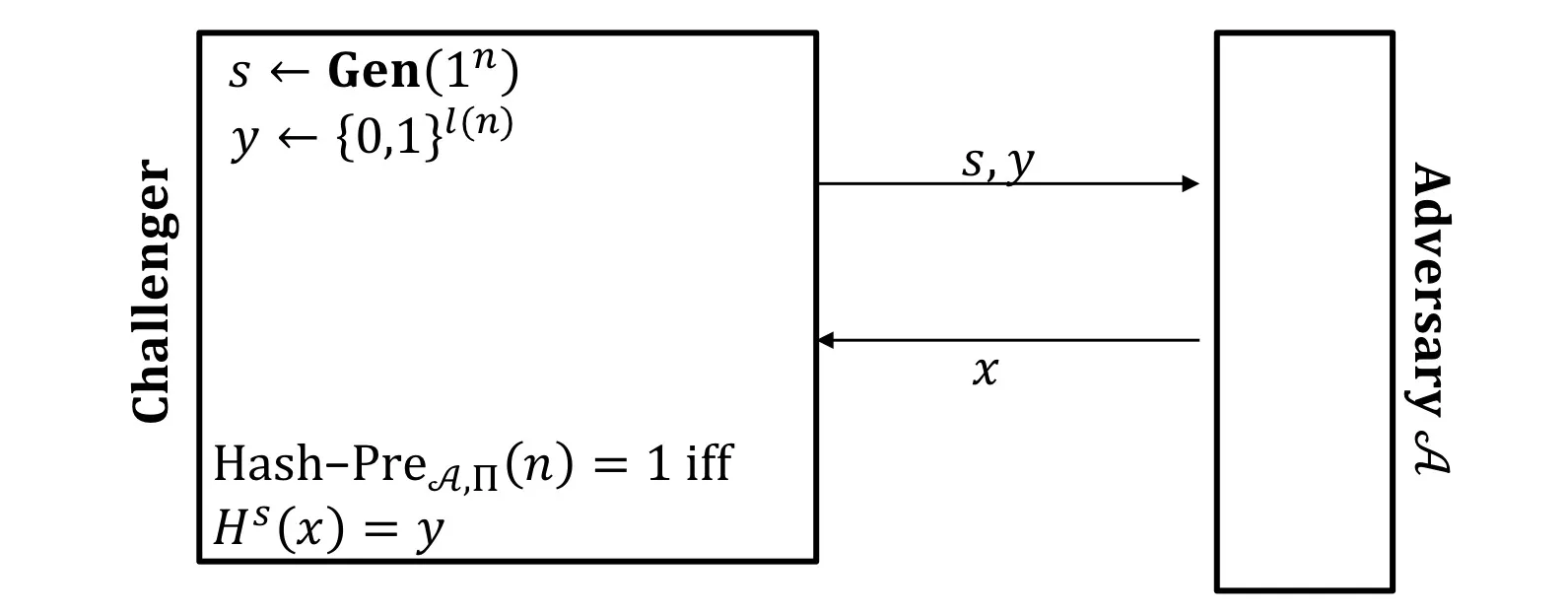
Collision resistant Second Preimage resistant
Second Preimage Resistant Preimage resistant
Merkle-Damgard Transform
Merkle-Damagard变换.
给一个定长的抗碰撞哈希函数, 可以制作出一个任意长度的抗碰撞哈希函数.
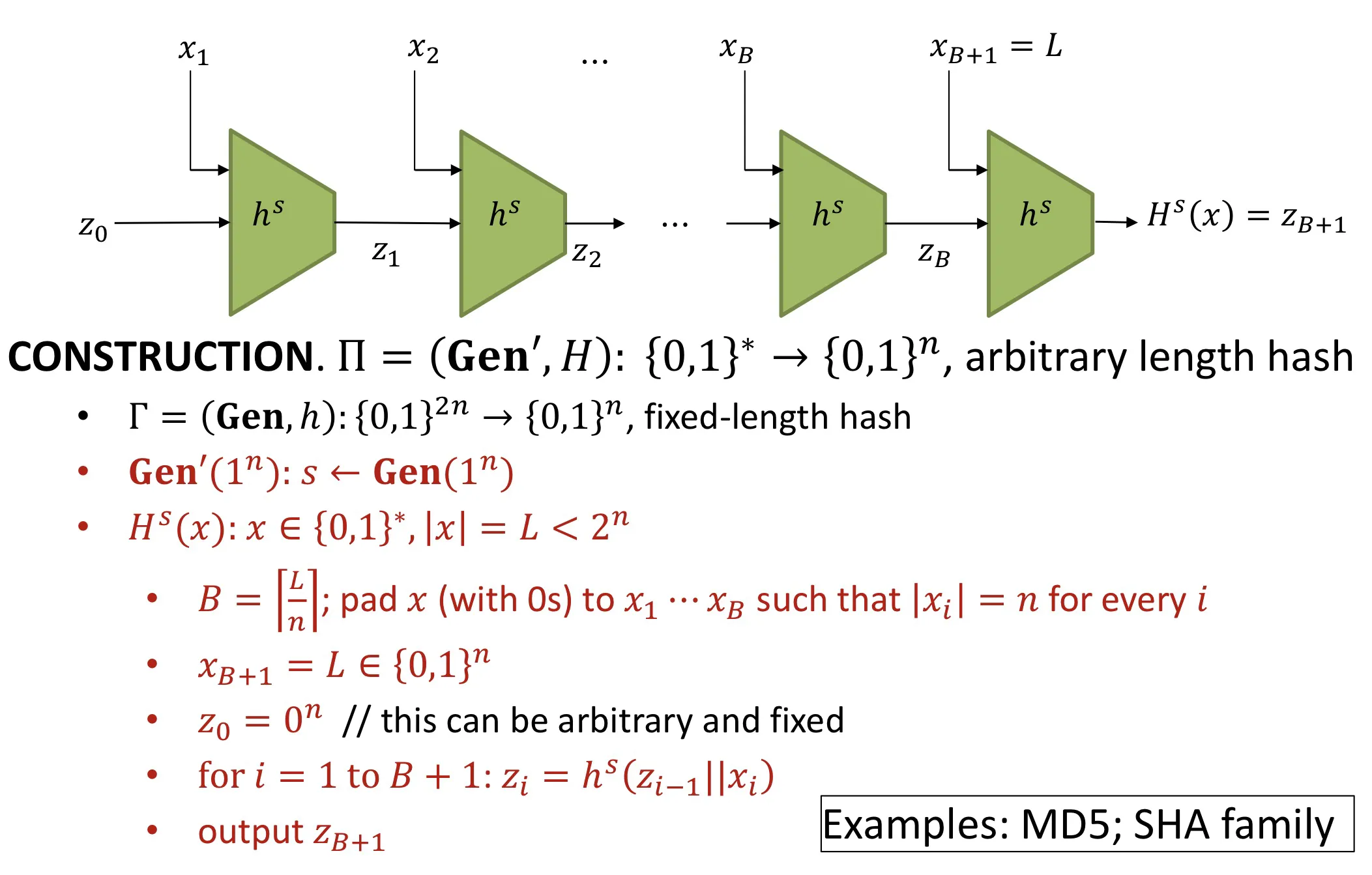
Theorem: If is collision-resistant, then is collision-resistant.
Lecture 14.
Hash-and-MAC
以前学的Arbitrary-Length MAC:
- MAC from PRF: , long tag, 效率低
- CBC-MAC: 取 IV=, short tag (t只取最后一块), 效率高一些, 但还是慢
Hash-and-Mac
// TODO
Lecture 16.


Lecture 17